Imagine uma aula em que os alun@s não apenas aprendem, mas vivem a matemática — onde conceitos abstratos se transformam em trocas reais, negociações e descobertas coletivas. No mundo ideal da educação, cada minuto em sala de aula é intencional, desde o primeiro "bom dia" até a reflexão final. Mas como transformar essa visão em realidade?
Hoje, você vai descobrir um planejamento estruturado em cinco etapas, pensado para aulas de Matemática do 7º ano, mas adaptável a qualquer componente curricular. Da acolhida que instiga a curiosidade ao ponto de chegada que consolida o aprendizado, cada passo foi desenhado para:
Conectar a matemática ao cotidiano (com atividades práticas como trocas de materiais);
Trabalhar habilidades da BNCC (como a EF07MA17, de proporcionalidade);
Engajar os alunos com metodologias ativas e problematização.
Se você já se perguntou como tornar suas aulas mais dinâmicas, significativas e menos dependentes do livro didático, este guia é para você. Vamos desvendar juntos como uma sequência didática bem planejada pode transformar 50 minutos em uma experiência memorável — e, quem sabe, inspirar seus alunos a enxergarem a matemática com outros olhos.
Preparado(a) para começar? Vamos lá!
1. Acolhida (3 minutos) – Preparando o Terreno
A aula começa com um momento de reflexão e ambientação. Enquanto a turma se organiza em quatro grupos aleatórios, questões provocadoras são lançadas:
"Como a humanidade comprava ou vendia antes de existir moeda oficial?"
"Já perceberam que algumas grandezas se relacionam? Por exemplo, se o número de seguidores de uma rede social diminui, o engajamento da conta cai."
"Será que podemos relacionar proporções? Por exemplo, duas balinhas podem valer um pirulito?"
"Se um pacote de figurinhas vem com 5 cards e custa R$ 2,00, quanto deveria custar um pacote com 15 cards, mantendo a mesma proporção? Será que sempre funciona assim na vida real?"
"Imagine que, em uma fábrica, 3 máquinas produzem 120 peças em 2 horas. Se uma máquina quebrar, como ficaria a produção? O que isso nos diz sobre a relação entre quantidade de máquinas e tempo?"
Essas perguntas estimulam o pensamento crítico e preparam os alunos para o tema da aula: proporcionalidade.
2. Despertando o Tema (7 minutos) – Aprendizagem Ativa na Prática
Aqui, entra uma metodologia ativa: os grupos recebem materiais escolares variados (lápis, borrachas, canetas) e devem negociar trocas, estabelecendo acordos justos.
Essa atividade simula situações reais de comércio e proporção, incentivando o trabalho colaborativo e a resolução de problemas. Ao final, cada grupo apresenta suas trocas, e a turma discute se foram equilibradas.
Roteiro para a Atividade de Negociação de Trocas (Duração: 7 minutos)
Objetivo: Os alunos vivenciarão negociações com materiais escolares, percebendo relações de proporção e valor em situações práticas, antes da formalização matemática.
1. Preparação (1 minuto)
O professor distribui kits de materiais diferentes para cada grupo (ex.: Grupo A recebe 4 lápis, Grupo B recebe 2 borrachas, Grupo C recebe 3 canetas, Grupo D recebe 1 caderno pequeno).
Explica a regra: "Cada grupo deve negociar com os outros para conseguir o que falta para seu kit ficar ‘equilibrado’. Vocês têm 5 minutos para fazer acordos justos!"
2. Negociação (4 minutos – Dinâmica Ativa)
Situação simulada:
Grupo A (4 lápis) quer borrachas, pois não tem nenhuma.
Grupo B (2 borrachas) precisa de canetas para anotações.
Grupo C (3 canetas) deseja um caderno para organizar as folhas.
Grupo D (1 caderno) está disposto a trocar, mas quer lápis para escrever.
Exemplo de diálogo entre grupos:
"Nós damos 2 lápis por 1 borracha. Aceitam?" (Grupo A para Grupo B)
"Não! Achamos que 3 lápis valem 1 borracha!" (Contraproposta do Grupo B)
"Ok, mas só se vocês também nos derem 1 caneta!" (Negociação incluindo outro material)
Papel do professor:
Circular pela sala, mediar conflitos (ex.: "Por que vocês acham que 2 lápis = 1 borracha é justo?");
Anotar acordos no quadro para discussão posterior.
3. Formalização das Trocas (2 minutos)
Cada grupo apresenta seu acordo final (ex.: "Ficamos com 1 lápis, 1 borracha e 1 caneta após as trocas").
O professor pergunta: "Algum grupo sentiu que ‘perdeu’ na troca? Por quê?" (Introduzindo noções de equivalência e proporção).
4. Por Que Essa Simulação Funciona?
Metodologia ativa: Os alunos aprendem fazendo, não apenas ouvindo.
Conexão com a matemática: As trocas serão convertidas em regras de três na etapa de Fixação (ex.: "Se 2 lápis = 1 borracha, então 8 lápis = X borrachas").
Engajamento: A disputa por "acordos justos" gera curiosidade para a teoria.
Dica: Se a turma for muito grande, use cartões com imagens dos materiais no lugar de objetos reais para agilizar.
3. Imersão no Tema (20 minutos) – Construção do Conhecimento
Nesta etapa, o professor conduz uma aula expositiva dialogada, trazendo exemplos de regra de três simples e mostrando como ela se aplica às trocas realizadas.
Exemplo 1: "Se 2 lápis valem 1 borracha, quantas borrachas valem 8 lápis?"
Exemplo 2: "Se 4 canetas são trocadas por 2 cadernos, qual a relação proporcional?"
A ideia é conectar a matemática ao cotidiano, usando situações que os alunos vivenciaram na atividade anterior.
Exemplo 1: Das Trocas em Sala para a Matemática
Contexto: Lembram da negociação em que 2 lápis = 1 borracha?
Problema: Se 2 lápis valem 1 borracha, quantas borrachas valem 10 lápis?
Resolução:
2 lápis —— 1 borracha
10 lápis —— X borrachas
2X = 10 × 1 → X = 10 / 2 → X = 5 borrachas
Discussão: "Se dobrarmos o número de lápis, o que acontece com as borrachas? Isso é proporcionalidade direta!"
Exemplo 2: Compras no Mercado (Proporcionalidade Direta)
Contexto: No mercado, 3 caixas de leite custam R$ 12,00. Quanto custariam 7 caixas?
Resolução:
3 caixas —— R$ 12,00
7 caixas —— X
3X = 7 × 12 → X = 84 / 3 → X = R$ 28,00
Discussão: "Percebam que, quanto mais caixas compramos, maior o custo total – isso é uma relação diretamente proporcional!"
Exemplo 3: Tempo e Produção (Proporcionalidade Inversa)
Contexto: Um robô monta 20 brinquedos em 4 horas. Quanto tempo ele levaria para montar 50 brinquedos?
Resolução:
20 brinquedos —— 4 horas
50 brinquedos —— X horas
20/50 = X/4 → (invertemos uma razão por ser inversa)
50X = 20 × 4 → X = 80 / 50 → X = 1,6 horas (ou 1h36min)
Discussão: "Aqui, aumentar a quantidade de brinquedos exige mais tempo – mas a relação não é linear! Isso é proporcionalidade inversa."
Dicas para a Aula:
Use tabelas no quadro para organizar grandezas (ex.: lápis × borrachas).
Pergunte sempre: "Se aumentamos uma grandeza, a outra aumenta ou diminui?" (para diferenciar direta/inversa).
Relacione com a atividade de trocas: "Lembram quando o Grupo A insistiu que 3 lápis valiam 1 borracha? Vamos calcular se isso era justo!"
Esses exemplos reforçam que a matemática está em tudo: desde um acordo entre colegas até compras ou produção industrial.
4. Fixação da Aprendizagem (13 minutos) – Individualização do Saber
Agora, cada aluno analisa matematicamente as trocas feitas em grupo, estruturando regras de três e verificando qual foi a troca mais vantajosa.
Essa etapa reforça a autonomia e permite que o professor identifique dúvidas individuais, ajustando a explicação conforme necessário.
Guia Prático para Análise Matemática das Trocas - (Passo a Passo para o Aluno)
Objetivo: Transformar as trocas negociadas em regras de três e descobrir qual grupo fez a troca mais vantajosa matematicamente.
Passo 1: Relembre as Trocas do Seu Grupo
Anote os materiais que seu grupo tinha antes e depois das negociações.
Exemplo:
Antes: 4 lápis + 0 borrachas
Depois: 1 lápis + 1 borracha + 1 caneta
Passo 2: Escolha uma Troca Específica para Analisar
Selecione um acordo do seu grupo (ex.: "2 lápis = 1 borracha").
Pergunte-se:
"Quantos lápis foram trocados por quantas borrachas?"
"Essa relação é justa? Como posso comprovar?"
Passo 3: Monte a Regra de Três
Use a proporção da troca para criar um modelo matemático.
Exemplo:
Se 2 lápis = 1 borracha, então:
2 lápis —— 1 borracha
X lápis —— 3 borrachas (se quisermos saber quantos lápis valem 3 borrachas)
Conclusão: 3 borrachas deveriam valer 6 lápis, não menos!
Passo 4: Compare com Outros Grupos
Verifique se outras equipes fizeram trocas diferentes (ex.: 1 caneta = 1 caderno).
Pergunte-se:
"Qual grupo conseguiu mais materiais proporcionalmente?"
"Se meu grupo tivesse feito a mesma troca, teria sido melhor?"
Exemplo de Comparação:
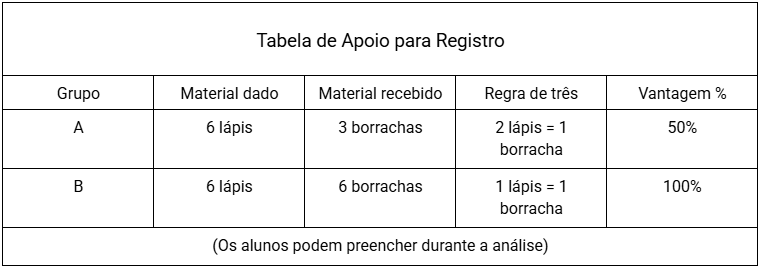
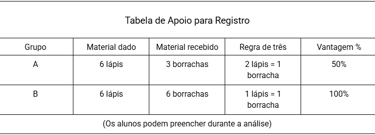
Grupo A: 2 lápis = 1 borracha → 6 lápis = 3 borrachas
Grupo B: 1 lápis = 1 borracha → 6 lápis = 6 borrachas (mais vantajoso!)
Passo 5: Conclua Qual Troca Foi Mais Vantajosa
Use cálculos para justificar:
Fórmula de Vantagem:
"Valor Relativo" = (Quantidade obtida / Quantidade dada) × 100
Exemplo:
Grupo A: (3 borrachas / 6 lápis) × 100 = 50% de retorno
Grupo B: (6 borrachas / 6 lápis) × 100 = 100% de retorno
Resposta: "O Grupo B fez a troca mais vantajosa, pois obteve o dobro de borrachas pelo mesmo número de lápis!"
Dica para o Professor:
Circule pela sala para ajudar alunos que tiverem dúvidas na montagem das proporções.
Destaque erros comuns, como inverter grandezas na regra de três.
Peça para compartilharem conclusões no final (ex.: "O Grupo C percebeu que aceitar 1 caderno por 5 canetas não foi vantajoso!").
5. Ponto de Chegada (7 minutos) – Reflexão e Consolidação
Para fechar, uma roda de conversa retoma o percurso da aula:
"Como as trocas iniciais se relacionam com a proporcionalidade?"
"Onde mais podemos aplicar regra de três no dia a dia?"
Esse momento valoriza a metacognição (refletir sobre o próprio aprendizado) e reforça a importância da matemática em situações cotidianas.
Estrutura do Diálogo Final:
1. Retomada do Percurso (2 minutos)
O professor resume as etapas, conectando-as à vida real:
"Hoje, começamos refletindo sobre trocas sem moeda (como no escambo), negociamos materiais em grupo, descobrimos a matemática por trás dessas trocas com a regra de três e analisamos qual foi mais vantajosa. Tudo isso está presente no dia a dia!"
2. Perguntas para Reflexão (3 minutos)
Questões que vinculam a aula ao cotidiano:
Sobre a Acolhida:
"Se antes trocávamos 2 ovos por 1 litro de leite, hoje usamos dinheiro. Mas como a regra de três aparece no preço dos produtos?"
(Ex.: Se 1kg de arroz custa R$5, quanto custam 3kg?)Sobre as Trocas em Grupo:
"Além de materiais escolares, onde mais fazemos ‘trocas’ invisíveis?"
(Ex.: Tempo × Dinheiro – "Se trabalho 2 horas para ganhar R$20, quanto ganho em 8 horas?")Sobre Proporcionalidade Inversa:
"Se aumentar o número de pessoas dividindo uma pizza, o que acontece com o tamanho do pedaço de cada um? Como calcular isso?"
3. Consolidação com Voz dos Alunos (2 minutos)
Peça que 1 aluno de cada grupo compartilhe:
"Uma situação cotidiana em que usariam regra de três."
"O que aprenderam hoje que não sabiam antes?"
Exemplos de respostas esperadas:
"Aprendi que promoções como ‘leve 3 pague 2’ usam proporção!"
"Entendi que, se meu celular carrega 20% em 30 minutos, carrega 100% em 2h30."
Frases de Fechamento:
"A proporcionalidade está nos pequenos e grandes momentos: desde dividir um lanche até planejar o orçamento familiar. Matemática não é só números – é entender o mundo!"
Sugestão de Ação Concreta:
"Desafio: anotem até a próxima aula onde viram regra de três no dia de vocês. Vamos compartilhar!"
Considerações Finais: BNCC e Metodologias Ativas
Este planejamento atende à habilidade EF07MA17 da BNCC, que prevê a resolução de problemas envolvendo proporcionalidade direta e inversa. Além disso, as metodologias ativas (como a negociação em grupo e a análise individual) tornam o aluno protagonista do conhecimento.
A aula proposta é dinâmica, contextualizada e humanizada, mostrando que a matemática não está apenas nos livros, mas em tudo ao nosso redor. E aí, profs? Que tal testar esse planejamento e adaptá-lo à sua realidade? Contem nos comentários como foi a experiência!
Referência Bibliográfica
BRASIL. Base Nacional Comum Curricular (BNCC). Educação Básica. MEC, 2018.